giftmeeting.blogg.se - U sub integration

InterSTO also have the same features as I mentioned below, whereas here the stocktransfer is 2 different company codes with different plants and each from onecompany code. Nowthe goods will be in in transit and the receiving plant person will be doingMIGO wrt PO, so that stock will show as unrestricted stock.Ĥ.Stocktransfer between two plants with delivery without billing (Intra STO) Usingmovement type 351-MB1B, movement of goods will happen once we create PO. Oncethe PO is created will give to the supplying plant and the from the supplyingplant there is a goods movement done by plant person. POwill be created with document category UB and item category as U, so that it’sa inter STO PO created for internal stock movement. This product is protected by copyright and distributed under licenses restricting its use, copying, distribution, and decompilation.See Also Plumber Fawn Creek KS - Local Plumbing and Emergency Plumbing Services in Fawn Creek Kansas 6 Biggest Problems Facing Businesses Today | The Kickass Entrepreneur 11 Revenue Models, Examples & Tips To Pick The Right One Borderline Personality Disorder

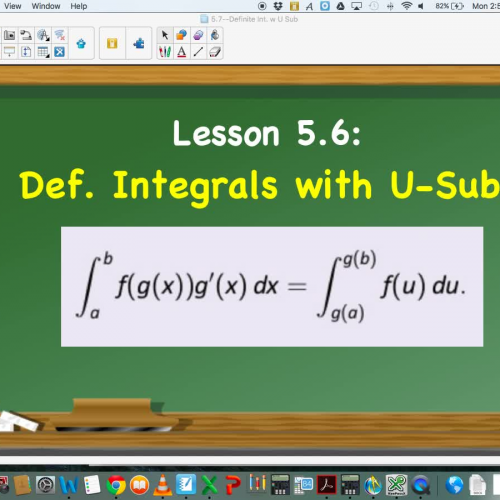
Prove that ∫ − a a f x &DifferentialD x = 0 for any odd function f. Verify that ∫ − &pi &pi sin x &DifferentialD x = 0, and that ∫ − &pi / 2 &pi / 2 cos x &DifferentialD x = 2 ∫ 0 &pi / 2 cos x &DifferentialD x. Įvaluate the definite integral ∫ 2 3 x 3 x 2 + 3 &DifferentialD x. Įvaluate the indefinite integral ∫ x 3 x 2 + 3 &DifferentialD x. Įvaluate the indefinite integral ∫ x 1 − 3 x 2 &DifferentialD x. Įvaluate the indefinite integral ∫ 2 x + 1 8 &DifferentialD x.

For the even function, the yellow and red regions match exactly, but for the odd function, the yellow and red regions match in magnitude, but differ in sign.Įvaluate the indefinite integral ∫ 3 x − 2 &DifferentialD x. In each case, the region shaded in yellow to the left of the y -axis represents the value of the definite integral on − a, 0 the region shaded in red to the right of the y -axis, the value of the definite integral on 0, a. Table 4.4.2 Definite integral of an odd or even function over a symmetric interval Table 4.4.2 details the value of a definite integral of an odd or even function taken over a symmetric interval such as − a, a. No matter how the substitution rule is given, an explicit solution for y = y x is needed for expressing the indefinite integral in terms of x.

In either of these cases, obtain dx by solving explicitly for x and differentiating, or by differentiating implicitly. Īlternate forms for the substitution are y = h x and r y = s x. If F y is the antiderivative obtained when the substitution x = g y is made in the indefinite integral, then F g − 1 x is an indefinite integral in terms of the original variable, x correspondingly, the value of the definite integral is given by F g − 1 b − F g − 1 a = F g − 1 x &verbar a b. Table 4.4.1 Substitution in definite and indefinite integrals ∫ a b f x &DifferentialD x = ∫ g − 1 a g − 1 b f g y &DifferentialD y ∫ f x &DifferentialD x = ∫ f g y g ′ y &DifferentialD y = F y = F g − 1 x Table 4.4.1 lists the rule for making a substitution, or change of variable, in an integral.